Among our crosswords and other puzzles, we’ll be featuring logic challenges from Puzzle Communication Nikoli, a cult-favorite puzzle publication from Japan. A PDF of the puzzle, as well as the solution, can be downloaded below.

For more than a century, one of the fundamental elements of modern puzzle-making is has been a shape made up of squares connected on their edges. In 1953, American mathematician Solomon W. Golomb gave them a name: polyominoes. Perhaps the most famous polyominoes are the two-square variety (dominoes) and the four-square configurations used in Tetris.

The readers and puzzle-makers behind Puzzle Communication Nikoli, the influential Japanese puzzle magazine, have long tried to use polyominoes in their puzzles—but it hasn’t been easy. In 1989, the magazine published a puzzle called Numbomino, which involved assigning numbers to squares and then totaling the numbers in each row and column. At the same, Nikoli puzzle makers were working with the four-color theorem, which states no more than four colors are needed to color a map so that no two adjacent regions are the same color (picture a globe, with four colors and no two neighboring countries have the same color).

The puzzle community behind Nikoli is constantly reworking, iterating, and improving their puzzles, and another theme that was starting to be used was tatami, the Japanese flooring mats that are laid out geometrically to cover a floor surface. Puzzle creators started messing around en masse with polyominoes, four-color theorem, tatami, and an existing puzzle called Shikaku. Nearly 10 new puzzles were published around this time, according to Nikoli president and puzzle-maker Yoshinao Anpuku. After five years of near-continuous improvement (including swapping numbers for colors, and deemphasizing the tatami arrangement aspects), Fillomino (as in, “fill” a “polyomino”) was born in 1994. Though it is credited to the Nikoli reader who goes by Suranta, it took trial-and-error from a lot of puzzlers to finally take shape.

Nikoli verterans, Anpuku says, were less than impressed. “I have seen it somewhere and it is not quite exciting,” many said, after all the iterations they had seen of the same idea. But Fillomino was such a perfect refinement that new readers of Puzzle Communication Nikoli made it a hit, and it’s been a fixture in the publication ever since.

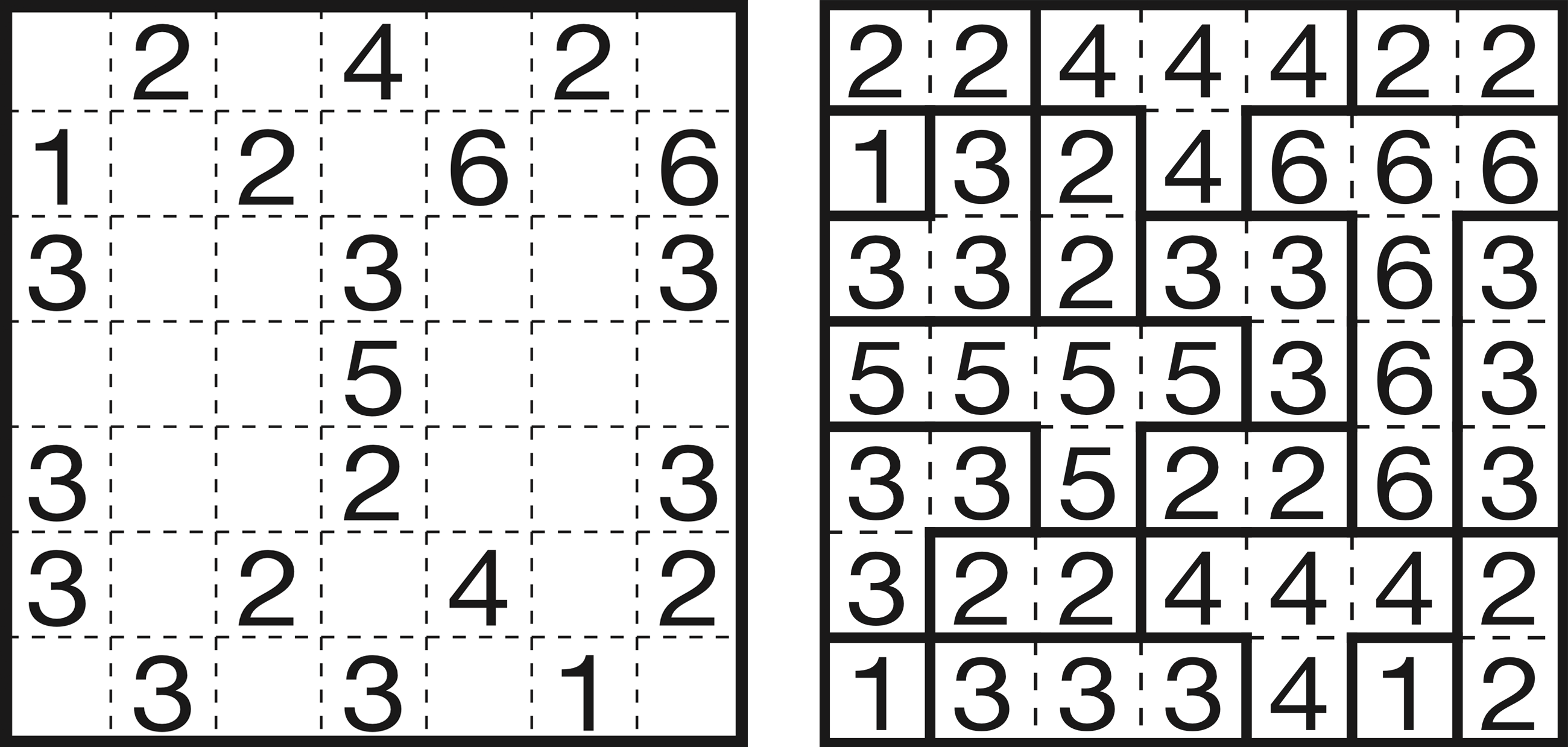
The goal of Fillomino is to create polyominoes of different sizes in a way that no two polyominoes with the same number of squares touch, and every cell in the grid is filled. It is also one of the few Nikoli puzzles—like Sudoku—that involves filling a grid with actual numbers. Each cell in a polyomino is filled with a number that reflects the total number of squares in it (i.e., a Tetris piece would consist of four squares, each containing the number 4). Solving it involves both filling in the numbers and outlining the shapes, making it a significant logical challenge.

Stumped? Download the solutions!